主页 > 生活 >
步骤
1
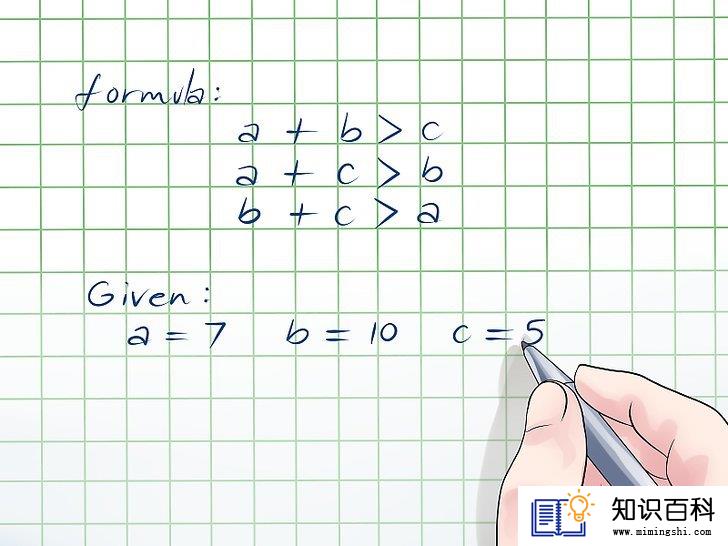
学习三角不等式定理。这条定理简单来说,就是三角形的两边之和永远大于第三边。如果这个定理适用于三边的任何组合,那么这就是一个三角形。你需要将这些组合一个个全都验证一遍,才能确定是否可行。假定三角形三边长度分别是a、b、c,那么这定理用不定式来表示就是: a+b > c, a+c > b, and b+c > a.
- 举个例子,a = 7, b = 10, c = 5.
2
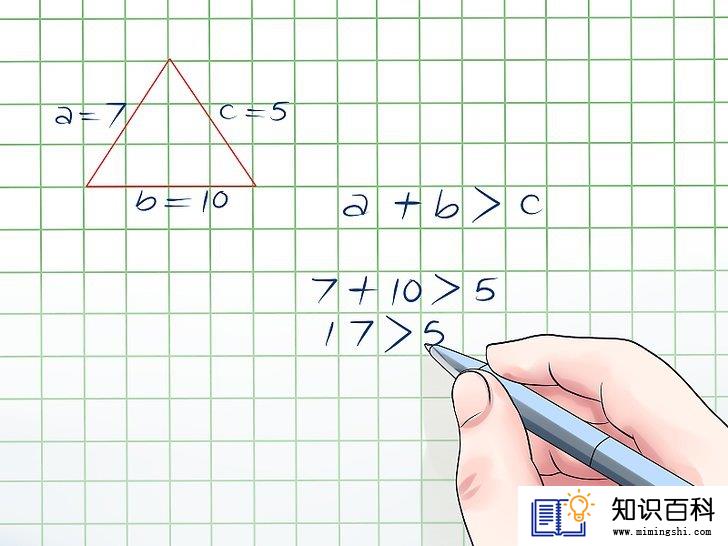
检查是否两边之和大于第三边。在上例中,你可以取ab之和,即7 + 10=17,17大于5,即17 > 5。
3
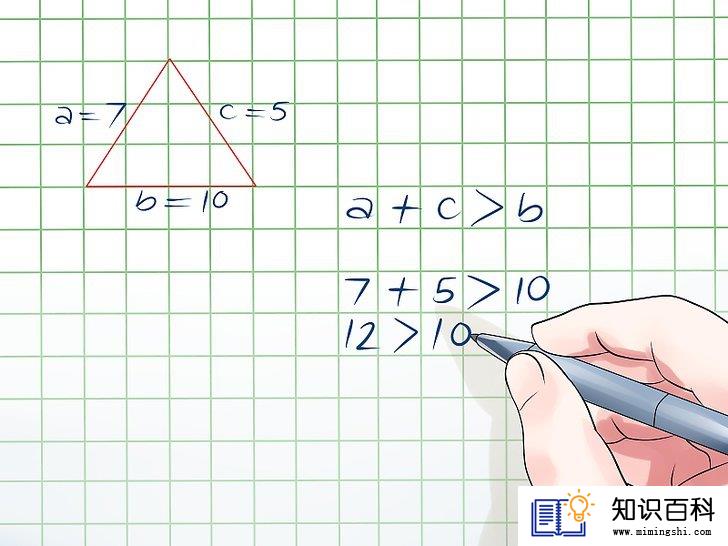
检查另外两边之和是否大于第三边。现在,可以看看ac之和是否大于b。也就是说看看是否7 + 5,即12大于10。因为12 > 10,不等式成立。
4
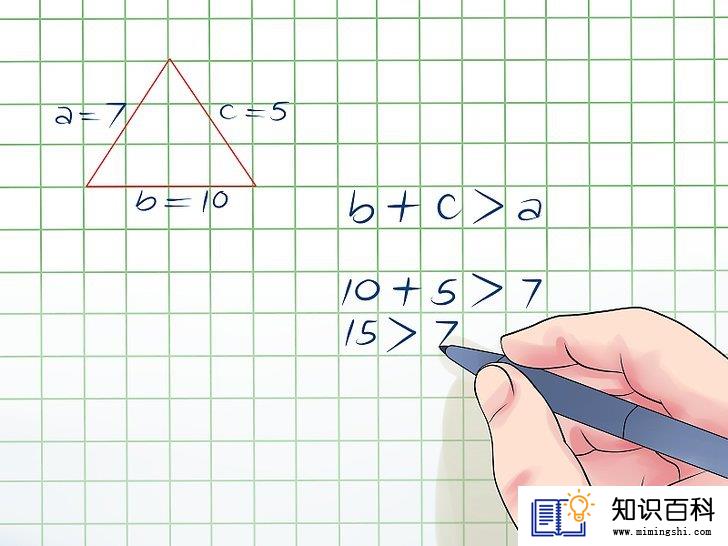
检查其它的两边之和是否大于第三边。你可以看看bc之和是否大于a。也就是说,你需要看看是否10 + 5大于7。10 + 5 = 15,而15 > 7,所以三角形所有边都验证通过了。
5
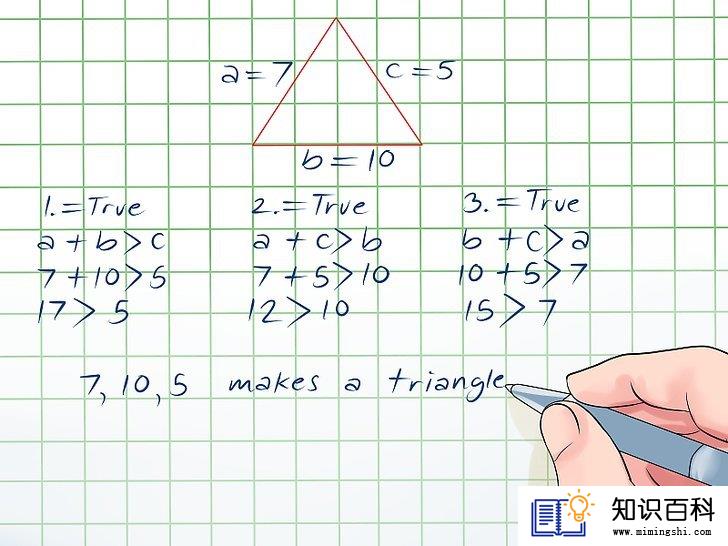
检查结果。现在,你已经把所有边的组合都验证过一遍了,你可以再检查一下,这条定律是不是三种组合都适用。如果对于这个三角形而言,在所有组合里,任意两边之和都大于第三边,那么该三角形是成立的。如果这条定律哪怕只在一个组合里不成立,那么该三角形就不成立。因为以下陈述都是成立的,那么这是一个有效的三角形。
- a + b > c = 17 > 5
- a + c > b = 12 > 10
- b + c > a = 15 > 7

6
学习如何指出一个无效的三角形。在练习里,你同样需要知道怎么指出一个无效的三角形。比如说,现在三边长分别是5,8,3。看看它是否能通过验证:
- 5 + 8 > 3 = 13 > 3, 所以一边通过。
- 5 + 3 > 8 = 8 > 8. 因为这不等式不成立,所以现在你可以停下来了。这个三角形不成立。
小提示
- 这个方法只要你没有算错,就不会有问题。它只需要最基础的加分,所以也非常简单。
- 上一篇:如何把二进制转换为十六进制
- 下一篇:没有了
- 01-23如何理解男人
- 01-23如何玩天堂七分钟
- 01-22如何找到你的精神动物
- 01-19如何煮玉米
- 01-19如何吃火龙果
- 01-16如何找到人生目标
- 01-19如何清洁鼠标垫
- 01-23如何成为好女朋友
- 01-18如何进美国的法学院
- 01-18如何计算出分数乘以整数的结果
- 01-18如何集中注意力学习
- 01-16如何有效地学习
- 01-16如何提高学习速度
- 01-16如何成为知识渊博的人
- 01-16如何学习基本英语
